Unendlichkeit
Wir sehen oben das Beispiel einer Mandelbrot-Menge. Sie ist benannt nach dem französisch-US-amerikanischen Mathematiker Benoît Mandelbrot. Die bekannte Darstellung resultiert aus einer iterativen (sich ständig vertiefend wiederholenden) Formel in der komplexen Zahlenebene:
Für jeden Punkt (c) startet man mit z0 = 0
und berechnet wiederholt
zn+1 = zn2 + c
Bleibt die Folge beschränkt (entfernt sich nicht ins Unendliche), gehört (c) zur Menge – visualisiert meist schwarz.
Egal wie stark man in diese unendlich komplexe Menge hinein zoomt, es wiederholen sich ähnliche Strukturen mit immer feineren Details. Die Grafiken dieser fraktalen Geometrie sind derart beliebt, dass sie sogar eine Bezeichnung im Volksmund erhalten haben, dort heissen sie "Apfelmännchen".
Die Mandelbrot-Menge verbindet Einfachheit mit unerschöpflicher Vielfalt und erzeugt atemberaubende, psychedelisch wirkende Bilder. Gleichzeitig ist sie Ausdruck einer rein mathematisch, prozesshaften Unendlichkeit: sie zeigt eine endlose Aneinanderreihung endlicher Schritte, die aber immer auf die geschaffene Ordnung bezogen bleibt und ihren Bezugsrahmen nicht verlässt.
Eine solche Unendlichkeit wird oft auch "schmutzige Unendlichkeit" genannt, was auf Georg Wilhelm Friedrich Hegel zurückgeht, der eine nicht endende Zahlenreihe, die sich aus ständigem Hinzufügen von "+1" erweitert, eine "schlechte Unendlichkeit" nannte. Eine solche Unendlichkeit, die rein aus Endlichkeiten zusammengesetzt ist, genügt dem denkenden Anspruch ans Unendliche nicht, da sie Unendlichkeit nicht positiv aufweist, sondern immer nur im Abgrenzung dessen, was sie nicht sein will: nämlich endlich.
Gerade in der modernen Science Fiction versucht man diesem Problem immer bildgewaltiger zu entgehen, indem man Spiegelwelten, ganze Multiversen und jegliche Art von bombastisch überzeichneten Illusionen schafft, die das Problem aber letztlich immer nur verschieben und nicht lösen. Wie weit mathematische Überlegungen gehen können, wird sehr anschaulich im sogenannten "Hilberts Hotel" aufgezeigt, einem Gedankenexperiment des deutschen Mathematikers David Hilbert.

Ein Hotel mit endlich viel Zimmern kann eine endliche Anzahl an Gästen aufnehmen. Hätte ein Hotel aber unendlich viele Zimmer, könnte es unendlich viele Gäste aufnehmen. Stellen wir uns also ein Hotel vor, mit unendlich vielen Zimmern, die alle belegt sind. Wenn nun ein weiterer Gast hinzu käme, was wäre zu tun um ihn aufnehmen zu können?
Die Antwort ist: Man lässt jeden Gast ein Zimmer weiter vor rücken, so dass am Eingang ein Zimmer frei wird, welches der neue Gast beziehen kann. Das kann man für jede beliebige Zahl erweitern, so dass man immer wieder neue Gäste aufnehmen kann.
Wie aber sieht es aus, wenn man in ein solches Hotel unendlich viele weitere Gäste unterbringen möchte? Wenn also ein Bus mit unendlich vielen Fahrgästen für jeden eine Unterkunft bräuchte? Hier ist die Antwort ein wenig komplexer:
Hier müsste jeder Gast in das Zimmer mit seiner doppelten Zimmernummer umziehen. Damit dies nicht unendlich lange dauert, müsste es allerdings exakt gleichzeitig geschehen. Da es sich bei der Verdopplung von Zimmernummern immer nur um gerade Zahlen handeln kann, bleiben die ungeraden Zimmernummern frei, was eine unendliche Menge an neuem Platz für den ankommenden Bus schafft.
Selbst wenn unendlich viele Busse mit unendlich vielen Fahrgästen kämen, wäre eine Belegung möglich, wenn man Gästen aus jedem Bus immer in Potenzen fortlaufender Primzahl-Nummern einziehen lassen würde. Gäste aus Bus 1 erhielten die Zimmer 3= 31, 9 = 32, 27 = 33, … Gäste aus Bus 2 die Zimmer 5, 25, 125... und so weiter. Auf diese Weise würden noch viele Zimmer leer bleiben, da ja nicht alle Zahlen Potenzen von Primzahlen sind.
An diesem Beispiel sieht man, wie weit man mathematisch tragbare Überlegungen im Raum der Unendlichen Zahlen anstellen kann. Dennoch verlässt man mit keiner Überlegung den Raum der "schmutzigen Unendlichkeit", da man es immer nur mit abzählbaren einzelnen Nummern zu tun hat, auch wenn es unendlich viele sind.
Das metaphysische Konzept der Ewigkeit
Georg Wilhelm Friedrich Hegel
Beginnen wir, weil er oben schon genannt wurde, mit dem Entwurf Hegels. Statt einer nicht endenden Reihe kann man sich sein System eher als einen geschlossenen Kreis vorstellen. Etwas wahrhaft Unendliches, so Hegel, müsse allumfassend sein, es dürfe kein Außen haben, von dem es sich abgrenzen könnte. Während klassische Konzepte von einem Gegensatz zwischen einem unendlichen Gott und einer endlichen Welt ausgehen, sah er in der Überwindung dieses Gegensatzes eine Einheit aus Gott und Schöpfung als Unendlichkeit an. Dies brachte ihm den Vorwurf des Pantheismus ein, der keinen Raum für individuelle Freiheit oder gar eine von der Welt unabhängige Identität Gottes lasse – wogegen sich Hegel jedoch stark wehrte. Er betrachtete die Einheit als konsequenten logischen Schritt, wenn man ausserhalb von Unendlichem nichts weiteres duldet. Damit rückt die Unendlichkeit aus der zeitlichen Ausdehnung hinein in eine zeitlose Präsenz in Richtung Ewigkeit.
Anicius Manlius Severinus Boethius
Gehen wir zeitlich einen Schritt zurück. Bereits im 6. Jahrhundert beschrieb der Philosoph Boethius das "Nunc Stans", also das "stehende Jetzt". Schon damals sah er die Ewigkeit nicht als unendlich lange Zeit, sondern als "den vollkommenen und gleichzeitigen Besitz unbegrenzten Lebens". (De consulaitone philosophiae/Trost der Philosophie, Buch V, Prosa 6, ca. 523/524 n. Chr.)
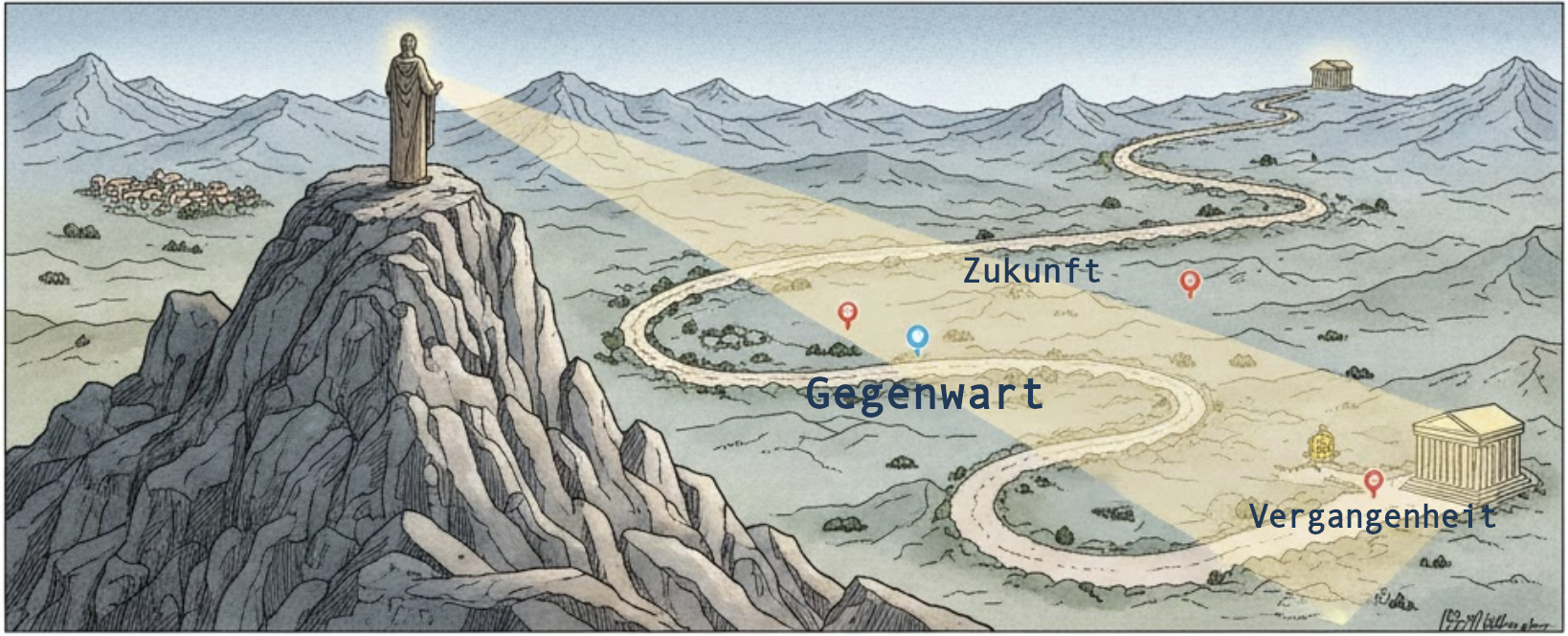

Gemeint ist hier, dass es eine übergeordnete Perspektive gibt, aus der man das Leben wie aus einer Vogelperspektive betrachten kann. Während wir direkt nur den vor uns liegenden Abschnitt sehen und uns an Vergangenes erinnern, kann von oben aus der gesamte Weg gesehen werden.
Platon und Aristoteles
Da wir mit Boethius bereits einen großen Schritt in die Vergangenheit gegangen sind, wagen wir noch einen weiteren Schritt bis in die Antike. Platon und Aristoteles als die großen griechischen Philosophen haben im Grunde bereits alle großen Themen aufgeworfen, die bis heute diskutiert werden – auch das der Ewigkeit. Ein kurzer Blick auf sie darf daher nicht fehlen.
Anfang der 2020er Jahre haben wir ein Video zu Platons Höhlengleichnis erstellt, das hier zu finden ist.
Bekannt ist seine Ideenlehre, die allem, was wir in der Welt erfahren oder erleben, eine Idee als Ursprung zuschreibt. Vor der Geburt haben wir demnach in einer Sphäre des Ewigen und Unveränderlichen existiert, als Seelen, die das Dasein in ihrer ganzen Fülle erfahren konnten. Leider ist diese Erfahrung bei der Geburt verloren gegangen, doch erinnert uns die Welt, in die wir gefallen sind, durch die Begegnung mit diesen Abbildern an ihren ewigen Ursprung. Sehen wir einen Tisch und unterscheiden ihn vom Bett, dann tun wir das, weil der Tisch eine Abbildung der Idee des wahren Tisch-Seins ist und wir, wenn auch schwach, an diese Idee erinnert werden, so dass wir intuitiv erfassen, was es mit dem Tisch (im Gegensatz zum Bett) auf sich hat.
Das oben erwähnte Höhlengleichnis veranschaulicht die Situation mit Menschen, die in einer Höhle eine Wand betrachten, auf die Schatten von Gegenständen projiziert werden. Die Gegenstände entsprechen den Ideen, die Schatten den auf der Erde erlebbaren Abbildern. Im Gleichnis schafft es einer der Betrachter, sich zu lösen und aus der Höhle zu entkommen, gar das Sonnenlicht zu erblicken, findet aber nach seiner Rückkehr keinen Anklang bei den anderen Bewohnern, die mit ihrer Sicht auf die Schatten zufrieden sind und den Blick auf die Wirklichkeit als Bedrohung empfinden.

Aristoteles hingegen geht das Thema nüchterner und weniger poetisch an. Er verlegt die Formen in die Dinge selbst und lehnt eine im realen Sinne vorhandene und vollendete Unendlichkeit als Vorstellung ab. Stattdessen sieht er eine Unendlichkeit der Möglichkeiten. Für ihn sind dies potentielle Unendlichkeiten, da Dinge ständig geteilt oder zusammengesetzt werden können. Das „Immer-weiter“ durch neue Kombinationen, diese prozesshafte Unendlichkeit, finden wir auch heute noch in der modernen Mathematik (Mandelbrot-Menge, Hilberts Hotel) wieder.
Theologische Aspekte
Auch wenn es heute in weiten Bereichen nicht mehr so gewürdigt, vielleicht auch gar nicht mehr erkannt wird: Die Theologie ist eine der großen Universalwissenschaften, denn grundsätzlich ist jedes Thema auch theologisch reflektierbar. Um so naheliegender ist dies, wenn es um Themen wie Ewigkeit, Unendlichkeit und damit natürlich um das Absolute geht. Wir beginnen den kurzen Einblick mit den wohl größten Theologen überhaupt, Augustinus und Thomas v. Aquin, machen dann einen großen Sprung zu C.S. Lewis als eher modernem Autor und enden in einer eigenen Schlussbetrachtung.

Augustinus von Hippo
Der Heilige Augustinus von Hippo (354–430) ist in vielfacher Weise ein Bindeglied zwischen antikem und christlichem Denken. Wir wollen uns in diesem Kontext vor allem auf zwei Aspekte beziehen: die Weiterführung Platons Ideenlehre zur Iluminationslehre sowie die Vertiefung des boethianischen "Nunc Stans" auf den persönlichen, lebendigen Gott.
In der Illuminationslehre, abgeleitet von dem lateinischen "lumen" (Licht), geht es um eine "Erleuchtung" während des Erkenntnisprozesses. Die unveränderlichen ewigen Wahrheiten Gottes strahlen in unsere zeitgebundene Welt ein und machen Erkenntnis dadurch überhaupt erst möglich. Damit christianisiert und personalisiert er Platons Ideenwelt: Die Ideen sind nicht mehr abstrakte Formen, sondern leben im Geist Gottes und leuchten dem menschlichen Verstand ein.
Gleichzeitig nimmt Augustinus Boethius’ „Nunc Stans“ auf und wendet es direkt auf Gott an. In den Bekenntnissen (Buch XI) beschreibt er Gottes Ewigkeit als ein zeitloses, immer gegenwärtiges Jetzt, in dem Vergangenheit, Gegenwart und Zukunft zugleich sind, während die geschaffene Zeit nur ein flüchtiges Nacheinander kennt.
Thomas von Aquin
Während Augustinus die Erkenntnis als ein direktes, beinahe übernatürliches Einwirken Gottes (Illumination) beschrieb, vollzog Thomas von Aquin im 13. Jahrhundert die sogenannte ‚aristotelische Wende‘. Er lehnte die Illuminationslehre zwar nicht rundweg ab, hielt sie aber für die normale menschliche Erkenntnis nicht für notwendig.
Die Ilumination sei sicher für Engelhierarchien gültig, als Menschen seien wir aber von der göttlichen Quelle des Lichtes derart weit weg, dass wir von diesem Licht kaum etwas abbekämen. Um die Wahrheit in ihren allgemeinsten Zügen erkennen zu können, habe Gott dem Menschen einen Leib verliehen, der durch den Geist, den intellectus agens, selbst als Licht, Teil unseres Wesens sei. Wir brauchen also keine ständige neue ‚Bestrahlung‘ von oben, um 1+1=2 zu verstehen; unsere eingebaute Vernunft reicht aus, um aus der Sinneserfahrung auf die ewigen Wahrheiten zu schließen.
Damit wird die Unendlichkeit bei Thomas weniger zu einem plötzlichen ‚Lichtblick‘, sondern zu einer logischen Schlussfolgerung. Durch die Beobachtung der endlichen Welt (Wirkung) schließt die Vernunft, indem sie den Ursachen nachgeht, zwingend auf den Anfang als erste unbewegte Ursache: Gott als reiner Akt (actus purus), der keiner Veränderung bedarf. Seine berühmte Definition der Ewigkeit lautet in diesem Sinne:
– Die Ewigkeit ist der endlose, zugleich ganze und vollkommene Besitz des Lebens.
Damit nimmt Thomas Boethius' "Nunc Stans" auf und macht es zur ontologischen Grundeigenschaft Gottes: Alles ist für Ihn gegenwärtig, ohne Vorher und Nachher.
C.S. Lewis
Einen modernen Zugang zur Frage nach Zeit und Ewigkeit bietet der Autor C.S. Lewis (u.a. Die Chroniken von Narnia). Er versuchte, das oft missverstandene Verhältnis der Dimensionen durch eine Analogie zu erklären. So beschrieb er unsere Zeit als eine gerade Linie, die auf ein Blatt Papier gezeichnet wird.
Die Linie
Sie repräsentiert unsere Zeitrechnung, hat einen Anfang und ein Ende. Wir Menschen befinden uns auf dieser Linie und können immer nur den Punkt sehen, an dem wir uns gerade befinden.
Das Blatt Papier
Das Blatt stellt die Ewigkeit dar. Die Linie ist zwar auf das Blatt gezeichnet, aber das Blatt selbst ist nicht einfach eine "längere Linie", sondern eine völlig andere, umfassendere Dimension.
Die Erkenntnis aus diesem Modell ist folgende: Gott (oder die Ewigkeit) ist nicht jemand, der an einem Ende der Zeitlinie steht und auf das andere Ende wartet. Er ist wie der Zeichner oder der Betrachter des Blattes, er hat die gesamte Linie – Anfang, Mitte und Ende – gleichzeitig im Blick. Das Blatt ist die Dimension, auf der Zeit überhaupt erst existiert.
Dieses Bild bereitet den Boden für ein weiteres berühmtes Gedankenexperiment vor: "Flatland". Es hilft uns zu verstehen, wie ein Wesen aus einer höheren Dimension (Ewigkeit) in unsere begrenzte Welt (Zeit) hineinwirken kann, ohne deren Regeln zu verletzen, während es für uns dennoch unfassbar bleibt.
Wer tiefer in die faszinierende Welt der Dimensionen eintauchen möchte, findet hier inspirierende Texte und Visualisierungen:
» Edwin A. Abbott: Flatland
Der Klassiker von 1884 im Volltext beim Projekt Gutenberg – eine satirische Erzählung über das Leben in einer zweidimensionalen Welt.
» Carl Sagan: Flatland-Erklärung (Video)
Ein legendärer Ausschnitt aus der Serie "Cosmos", in dem der Astronom Carl Sagan mit einfachsten Mitteln erklärt, wie wir uns eine vierte Dimension vorstellen können.
» Die Visualisierung des Durchbruchs
Die Original-Illustration(Wikipedia): Eine Kugel (3D) tritt durch eine Ebene (2D) und erscheint dort als wachsender und schrumpfender Kreis.
Diese Konzepte verdeutlichen: Was uns als Wunder oder Paradox erscheint, könnte aus einer höheren Perspektive schlicht die logische Beschaffenheit einer umfassenderen Realität sein.
Fazit
In der Regel werden die Begriffe Unendlichkeit und Ewigkeit gern synonym eingesetzt. Spekulationen über Anfang und das Ende unseres Daseins, wilde Konstrukte mit denen wir scheinbar simple und überholt wirkende Überlieferungen wie die eines Schöpfergottes oder des Urknalls als Anfang des Universums überbieten wollen, entpuppen sich nicht selten als Spielarten schmutziger Unendlichkeit, auch wenn sie in lautem und farbigen Gewand, als Blockbuster oder neue physikalische Theorie verkauft werden. Mit großem Selbstbewusstsein vorgetragen erreichen sie oft nicht die gedankliche Tiefe von Schriften, die mittlerweile hunderte oder gar tausende Jahre alt sind.
Dennoch gibt es auch die leisen Töne, die Vertiefung und Weiterführung der Erkenntnisse unserer Ahnen. Hier wird immer wieder der Versuch unternommen, neben der Unendlichkeit auch die Ewigkeit zu umreißen und immer wieder wird auch festgestellt, dass wir das aus unserer Person heraus nicht befriedigend bewerkstelligen können. Wir können Grenzen unseres Denkens aufzeigen, wir können Analogien aus dem schließen, was wir erfahren, aber wir werden keine positive Definition von Ewigkeit geben können.
So bleibt das theologische Deuten auf etwas Größeres. Wir können von der Ewigkeit als Überbietung der Raumzeit sprechen, als ein Aussen, welches unseren Erfahrungsraum erst ermöglicht hat, ein Alpha und ein Omega, welches nicht den ganzen Weg durchlaufen muss, da es perspektivisch alles auf einmal im Blick hat. Vielleicht kann man von dort aus auch erahnen, was die christliche Botschaft bedeutet, wenn sich der Schöpfer selbst, aus hingebungsvoller Liebe zu seinen Geschöpfen, auf den Weg gemacht hat, eben dieses zeitlich und räumlich begrenzte Leben mit uns zu durchwandern, so dass er sich ganz auf unsere Perspektive eingelassen hat um alles mit uns zu teilen.
